More on distillation
Following on from the article that introduced the concept of distillation via the ancient process to produce whisky, this is a basic primer I drafted based on techniques used for distillation design prior to the advent of powerful commercial software running on personal computers in the early 1980s.
Designing a distillation column design using a simulator such as Aspen HYSYS or Honeywell’s UniSim can sometimes be challenging for the inexperienced and requires a different skill set. Provided the starting point is reasonable, the simulation software will iterate and normally converge quickly on a rigorous solution.
The older techniques are fairly simple and largely manual using graphical representations. However, they may provide some useful insight and perspective lost to the current and future generations of process engineers, and thus complement their use of the powerful tools in the simulators.
The main graphical techniques are limited to binary (2-component) mixtures, although they can sometimes be adapted to model more components with sufficient accuracy to put the process engineer in the right ballpark to use the simulator.
Introduction
Distillation is the most widely used technique for separating mixtures of distinct chemical species by virtue of their differences in volatility (comparative tendency to vapourise).
Prior to the advent of powerful computer software, an engineer had to delve into the basic detail behind a distillation process to find reasonable values for the main design parameters - reflux ratio, number of stages etc. T. The object of this article is an overview and perhaps a refresher for some on these basics of distillation separations.
In its simplest form - a 2-phase (vapour and liquid) mixture of 2 or more components, the components may be partly segregated by simply separating the vapour from the liquid in a vessel. The vapour has a higher concentration of the Most Volatile Component(s) (MVC) than does the liquid. The other usually heavier component in a binary is denoted Least Volatile Component (LVC). The liquid is somewhat enriched in the LVC and depleted in the MVC.
This basic phenomenon that enables partial separation of two distinct species by virtue of their different volatilities is extended to provide a linked cascade of separation steps enabling a successively more complete separation between the main components. The physical equipment for this cascade is what we know as a distillation column. For more description of this see a later section on hydraulic design.
Equilibrium K-values
When the two phases are at the same temperature and pressure and their concentrations are not changing, they are considered to be at equilibrium. The ratio of molar concentration of a component in the vapour (denoted ‘y’) to its concentration in the liquid (‘x’) is the equilibrium ‘K-value’ for that component.
Thus Ki = yi / xi. - (1)
In an ideal mixture, we can use two well-known laws to easily estimate the K values.
1) Raoults Law: Partial pressure of component i, Pi = xi . Pi* - (2)
Where Pi* is the pure vapour pressure of i at the system temperature,
2) Daltons Law: Partial pressure of component i, Pi = yi . PT - (3)
Where PT is the total system pressure.
Combining these we obtain yi . PT = xi . Pi*, so Ki = (yi / xi) = Pi* / PT - (4)
(Note vapour pressure, partial pressure and total pressure are all absolute, NOT gauge pressures).
The simplest and most frequent mixture to be separated by distillation consists of two components - called a binary mixture. The relative concentrations of the MVC in the vapour and liquid are conveniently shown on an X-Y diagram, and this can be used to trace the steps in a distiilation process that separates them.
Volatility and Relative Volatility (Alpha, αij )
The most volatile (usually the lightest or lowest molecular weight) component has a higher K-value than the least volatile (usually the heaviest) component. The ratio of a given component K value to that of the heaviest component is usually termed α (alpha) the relative volatility. αij.is the volatility of component i to that of the ‘base’ component j.
αij = Ki / Kj - (5)
In a binary 2-phase mixture the MVC has a K value greater than 1 and the LVC a K value less than 1.
Thus α-MVC is >1 and α-LVC = 1.0.
As shown above, the K values of components in an ideal mixture at a certain temperature T and pressure P are found from the (pure component vapour pressure at T) / (total pressure, PT).
That is Ki = Pi*/PT. (Note: in reality this is an approximation and only valid for ideal solutions).
Therefore since αij = Ki / Kj , we can write αij ~ Pi* / Pj* - (6)
It is found that, although vapour pressure P* and therefore K values change significantly with temperature, to a reasonable approximation, the ratio of P* (LVC to MVC) and therefore the ratio of K values or alpha (αij ) does not change very much.
So, for a many preliminary calculations of a binary (2 component) mixture a single effective average value of alpha (MVC) may be used, remembering that alpha (LVC) = 1.0.
Use of Alpha in phase equilibrium
How is alpha used in phase equilibrium calculations?
For a binary mixture, we know that yi + yj = 1.00 and xi + xj = 1.00 (7a), (7b)
So, because yj = (1 – yi) and xj = (1-xi), we can combine with eqns (1) and (5) to obtain
yi = αij. xi / (1 + xi(αij – 1)) - (8)
The Y versus X graph called a McCabe-Thiele plot may be used together with so-called operating lines to step off the number of equilibrium stages needed for the separation.
To carry out the graphical stepwise calculation of the number of theoretical stages required for the distillation, some additional information has to be defined in addition to the equilibrium x-y curve.
These additional items are:
• Product compositions (in terms of MVC concentration in distillate and bottoms)
• Feed composition
• Feed quality (liquid fraction)
Based on these, the minimum reflux ratio (infinite number of stages) may be determined.
Also the minimum number of stages required at total reflux.
Between these two limits, a practical and viable optimum reflux ration and number of stages may be found. Two common relationships are available to estimate the number of actual stages at a given reflux ratio
These are the Erbar-Maddox chart and the older Gilliland chart.
Product Compositions
The top and bottom product compositions are conveniently both defined in terms of the concentration of MVC, Yd and Xb respectively. Together with the feed composition, z, the overall column material balance is established. This is summarised for a worked example below.
Overall balance: F = D + B - (9)
MVC balance: F.z = D. yD + B. (1 – xB) - (10)
Combining (9) and (10) gives D = F. (z - xB) / (yD – xB) - (11)
Feed condition or ‘q’ value
The feed quality, is defined by the value of q. Stated simply q represents the liquid molar fraction of the feed.
For a feed that is 100% saturated liquid q = 1; for saturated vapour q = 0; for a 50/50 vapour liquid mix q = 0.5.
More generally, q can be expressed as the energy needed to produce saturate vapour feed divided by the latent heat of vaporisation of the feed. This means that for a superheated vapour feed q is negative, and for a subcooled liquid q is greater than 1.
On a McCabe-Thiele x-y diagram the ‘q line’ starts on the 45° line, x = y at feed overall composition, z and intersects with the equilibrium line at xf , yf which are respectively the mol fraction of MVC in the liquid and vapour portions of the feed. This is found as follows:
The q line has the straight line form y = m.x + c.
It has a slope, m = – q / (1- q) and passes through x = z, y = z,
so the intercept c = z / (1 - q)
Therefore the q line is: y = - q . x / (1- q) + z / (1 – q) - (12)
or y = (z – q.x) / (1-q) - (12A)
The q line intersects with the equilibrium line where:
yf = αij. Xf / (1 + xf(αij – 1)) = (z – q.xf) / (1-q) - (13)
xf = (-b – sqrt(b2 – 4.a.c)) / (2.a)
where b = αij . ( q = z – 1) – (q + z)
a = q. (1 - αij)
c = z
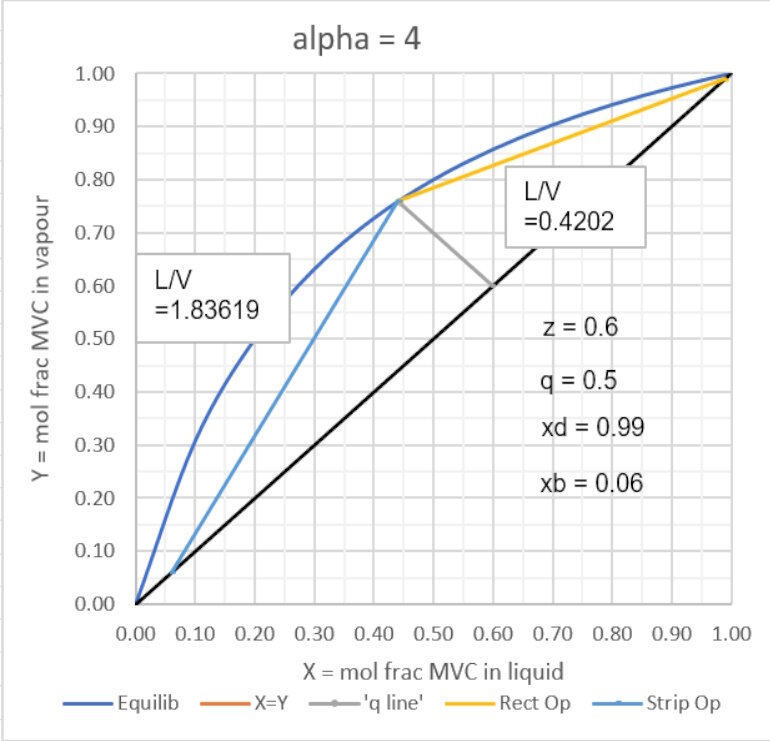
The graph below shows yi as a function of xi for a value of αij = 4,
and the q line for z = 0.6, for which xf = 0.4408; yf = 0.7592
The above diagram was generated in Excel based on the relationships described above. This makes it easy to see the effects of change in the alpha value, the feed compsition or ‘q’ value and the product purities on the minimum and maximum (L/V) values for the top (rectifying) section and the lower (stripping) section
Minimum Reflux ratio
Reflux ratio can be defined in 2 principal ways:
The External Reflux Ratio = (Liquid reflux flow / Distillate flow), R = L/D
The Internal reflux ratio = L/V.
The internal reflux ratio is more useful as it represents the slope of the operating lines above and below the feed, respectively (L/V) and (L’/V’).
The Enthalpy Composition diagram
This approach developed by Ponchon and Savarit and widely used by Ruhemann and others including the author, presents more information than the X-Y McCabe-Theile diagram, specifically the column energy balance.
A typical binary mixture enthalpy composition diagram.
This shows equilibrium tie-lines linking the equilibrium vapour and liquid compositions, the liquid and vapour enthalpies, a 2-phase feed (approximately 30% liquid) with composition Z and enthalpy h and an operating line at minimum reflux producing 2 essentially pure products.
The ‘delta point’ D coordinates are the overhead distillate composition (Yd ~ ) and the enthalpy flow up the column. This is the sum of the overheads enthalpy plus the condenser duty per mol of distillate. Similarly ‘delta point B’ coordinates are the bottoms composition (Xb~0 in this example) and the bottoms enthalpy minus the reboiler duty per mol of bottom product.
When H-X-Y data is available it can be used (optionally with a superimposed a T-X-Y plot) to present visually the minimum reflux ratio and actual heat addition to - and removal from the column system in reboiler and condenser and assess the number of stages and their temperatures. These can then be used as starting points for a riogorous computer simulation.
The H-X-Y diagram can also assess the scope for side-reboilers and condensers, which improve a column’s thermodynamic effciency.
Other topics in completing a distillation column system design are introduced briefly here.
Space and time prevent a detailed description:
These are:
Distillation Column Control
Hydraulic Design
Condenser and reboiler design
Distillation column control
This is often not straightforward and needs some care to ensure the column fulfills its designed performance.
Some issues are discussed below.
The picture above shows a distillation column reflux system with some typical control loops.
The basic arrangement shown is to give a constant reflux flow. If the overheads flow increases, the temperature would tend to increase. The reflux drum TIC should cause an increase the condenser fan speed until at max. However, the extra liquid condensed will all appear as increased product via the LIC valve opening.
To maintain product purity - all else being equal - it would be necessary to increase the set point of the reflux FIC to give a constant internal reflux ratio of L/V. This indicates a more complex control scheme may be necessary to keep purity steady.
One solution is to sense the temperature a few trays below the top and use this as a surrogate for an increase in temperature profile in the top of the column - requiring an increase in reflux. This additional TIC (shown) would be cascaded onto the Reflux FIC controller. The optimal PID (proportional, integral and derivative) control parameters would be pre-set using rules of thumb and dynamic modelling and finalised during commissioning.
One other point - due to its location, the drum TIC may be slow to respond and a better location would be in the liquid line from the overheads condenser.
A further parameter not so far discussed is the column pressure. If purity of product and condenser temperature are both maintained then this determines the pressure. However, it is common practice with a partial condenser, to use a pressure controlled vent of the vapour in the reflux drum to control column system pressure.
Hydraulic Design
To understand the hydraulic design it is helpful to revert to the basic concept of the distillation cascade.
The cascade of steps in a distillation column are often considered as and termed ‘equilibrium stages’. An equilibrium stage - let’s say stage ‘N’ is equivalent to the separator pot as described in the introduction, where liquid and vapour phases are separated. The vapour leaves the top of the ‘pot’ somewhat enriched in the lighter (more volatile components) and the MVC-depleted liquid leaves the bottom of the pot.
The vapour leaving the pot passes as a feed to the stage (N-1) above, and the liquid passes to the stage below (N+1).
By the same token, the feeds to stage N are liquid from the stage above (N-1) and vapour from the stage below (N+1). The function of the equilibrium stage (N) is to intimately mix these two vapour and liquid phases such that their compositions come to equilibrium, and then to separate them as described above.
Liquid (blue) and vapour (red) flows between two equilibrium stages (trays).
The vapour passes through small holes in the sieve tray where it mixes with and comes to equilibrium with the liquid. The liquid passes to the tray below via a segmental down comer.
The column physical size (diameter and height) is determined by the hydraulic design. This must consider several factors relating to the passing streams of vapour and liquid. Some considerations are:
The column net flow area for the vapour must be sufficient that liquid droplets are not entrained and carried to the tray above. This risk is reduced if the spacing between trays is increased.
After contact with bubbling vapour on the tray, the liquid flows over a weir and into the downcomer. The exit weir height determines the effective depth of clear liquid on the tray. In addition the height of liquid over the weir depends on its length.
Part of the column cross section is occupied by these segmental liquid ‘downcomers’. These must be adequate in size to allow the foaming liquid to collapse before it enters the tray below. The clearance at the downcomer bottom should be not more than the weir height, to ensure a seal, but must not restrict the liquid flow causing it to ‘back-up’ to the tray it is leaving.
If the vapour velocity is low for example on turndown, or the tray perforations are too large, some liquid can ‘weep’ through the holes in the tray. This bypassing liquid stream adversely effects the separation performance of the distllation.
Conversely if the vapour velocity is too high, the pressure drop of vapour passing through the perforations (called the dry tray pressure drop) may restrict the ability of the liquid to flow from one tray to the next causing downcomer backup.
The column internals can differ from the standard sieve tray, such as bubble caps and valve trays which autmatically close on low throughput to prevent weeping. Structured packing is also commonly used instead of trays on some air separation columns. The basic principles of counter-current liquid and vapour flow with component mass transfer between the phases still apply.
The iterative process to produce a design that satisfies the hydraulic constraints for all operating cases envisaged is best done by computer - either using Excel, or by the process simulator.